How Asymetric Encryption Works
In a few previous articles I have explained why encryption may be important to you and how the theory behind encryption works. I did not yet explain the system of asymetric cryptography, however. That is what this article is for.
Previously, we talked about how symetric encryption works. This is by having a shared key that both parties use to simultaniously encrypt, and decrypt the data. (See Ceasar Cipher for example).
Public-key, or Asymetric Encryption
Asymetric encryption is based on the idea of having multiple keys instead of only one shared key. For example: instead of encrypting with one key, and decrypting with that same key (like our ROT ciphers we talked about previously), we can use one key to encrypt the information, and a different key to decrypt the information.
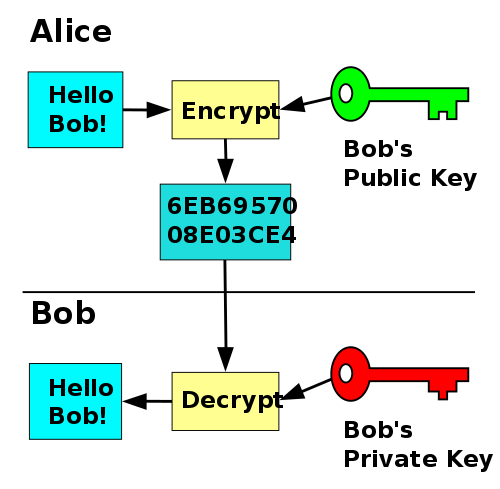
In the picture above, see how Alice uses Bob’s public key to encrypt some data, then sends it to Bob for him to decrypt with his private key? That is the essense of public-key encryption.
The great thing about public-key encryption is that your public key is public! There is no need to be afraid of sending this everywhere! You can attach it at the end of all your emails, the end of your forum posts, a link to it on your low-power webserver (wink). There are even things called keyservers that will save your public key on them for retrival in case somebody wants to verify your public key.
Anything encrypted with your public key can only be decrypted with your private key. Provided you never, NEVER share your private key with anyone ever, we can assume that all messages sent to you encrypted with your public key will never be read by anyone else.
Asymetric encryption, however, often contains four keys instead of two. Why is this?
Verification of Author
One interesting thing about keys pairs is that not only can the private key decrypt anything the public key encrypts, but the public key can decrypt anything the private key encrypts.
Now why would one want to encrypt a message that can be decrypted by anyone?
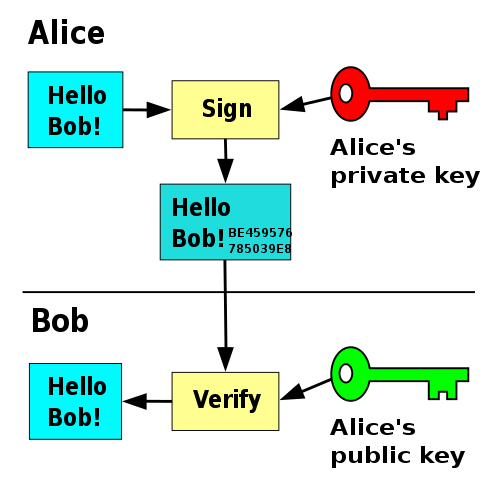
Note: Although the picture shows otherwise, the text is not sent in the plain. It is encrypted with Alice's private key.
This is how you can verify that the person who says they wrote the message really did indeed write the message! If their private key was never shared with anyone else, then the message must have come from them!
For maximum security, these methods are often layered. First, signing with the sender’s private key, ensuring only they could have sent it— then encrypted with the recipient’s pulbic key, making sure only the reciever can read it.
Note that both sides must first have eachother’s public keys to do this. This is easy if they communicate often, but when first contacting somebody, people will generally send their encrypted message along with the their own pulbic key attached in a seperate file.
What This Means
Notice neither Alice nor Bob had to share any comprimsing information over the network? This is why public-key encryption is so powerful!
Alice and Bob can both safely send their public keys in the open. They can even send them over the insecure HTTP, or FTP protocols.
Whilst not sending any encryption-breaking messages, Alice and Bob now have a way to communicate securely. If you trust nothing and no one, this is your perfered method of security.
Check out this Computerphile video if you want the simplified explaination.
The Algorithms
The two biggest “implementations” of public-key cryptography vary only in the mathamatical equations used to generate the numbers, and how the numbers are “trapdoored” to decrypt if you have the correct key.
I will discuss the differences in approach here. If you want to skip to the next article where I show you how to encrypt your own documents using RSA, see this link.
RSA
The mathamatic center of the RSA system was developed over the course of a year or so. Three men were involved. Ron Rivest, Adi Shamir, and Leonard Aldeman. They worked as a kind of “team”: Each idea by Rivest and Shamir were critisized by the mathamatician on their team: Mr. Aldeman.
One night, after consuming “liberal quantities of Manischewitz wine” Rivest had trouble sleeping. After taking long gazes into the abyss of his math textbook, he came up with an idea which would change cryptography forever. By the next morning, an academic mathamatical paper was nearly finished. He named it after himself and the two others that had been helping him along this whole time. Rivest, Shamir, Aldeman.
Key sizes of RSA range from 1024-bit to 4096-bit. 1024-bit keys are considered somewhat insecure. However, it should be noted that every bit doubles the complexity of the key, so 2048 is 2^1024 times more complex than 1024.
Eliptic-Curve (EC)
Eliptic-Curve (EC) is a family of algorithms that use the Eliptic curve mathamatical structure to generate the numbers for the keys. EC can effectivly provide the security of an RSA key one order of magnitude larger than an RSA key.
It’s fast; it’s secure! Perfect right?
Of course not!
One problem is that due to the smaller key size, it can more easily be broken by brute-force. This is why EC is mostly used for temporary communication (like HTTPS), not permenant communication (like having an encrypted email conversation with a journalist).
The other problem is that a certain EC algrorithm called P-256 is suspected to be introduced with malice to National Institute of Standards and Technology (NIST) by the NSA. Supposedly, the NSA is able to crack anything encrypted with this algorithm. I will let the experts argure about that.
Other well-known EC algorithms that are more-or-less trusted as secure do exist though. The premeire one being Curve25519. The reference implementation of this algrorithm is also public-domain, so it is easy for devlopers to work into their own applications without worrying about copywrite.
Conslusion
In this article we went over some basic points:
- Public-key encryption enables secure communication over insecure networks.
- RSA is considered the standard for extra-seure communication.
- EC is a newer, faster, more transient encryption method.
To learn how to use RSA keys to encrypt your own communications, check out this other aritcle I wrote.